 807
807
 2025-01-13
2025-01-13
中国粉体网讯 粉体颗粒概述
粉体颗粒一般认为是由大量常规操作及分散条件下不可再分的固体颗粒聚集而成,其内部存在大量空隙,属于复杂的多相系统,如日常生活中常见的土壤、砂石、积雪等。
粉体颗粒单独来看是由小颗粒组成,既具备固体的抗变形能力等,因此便于对粉体颗粒进行进一步的加工操作;粉体作为聚集体,又具备了液体一样的可流动性,便于对其进行运输;同时粉体还具有气体的可压缩性及可分散性,这就使得粉体具有较大的比表面积,从而能充分与周围环境直接接触,可以增大比表面积,有助于促进相关反应的进行。因此也有学者认为粉体是一种新的物质形态。
目前针对粉体颗粒大小的划分并不统一,一般可分为三类。粒径在20~200微米的颗粒称为细粉;粒径在3~20微米的颗粒称为微粉;3微米以下的颗粒称为超细粉体。
粉体压缩基本理论
由于粉体颗粒的离散特性,导致其在自然堆积状态下体系内部会存在一定的空隙,使得粉体具有一定的可压缩性。在外加负载作用下,粉体能够变得密实甚至被压缩成具有一定形状和强度的产品。粉体这一压缩变化过程,大体可以分为以下三个阶段。

颗粒所受压力与密度变化曲线
初始阶段,受压颗粒发生重新排列,受压颗粒间会相互靠近使接触面积增加,大量颗粒会发生滑移、转动现象。这一过程会使被压缩粉体原有的内部稳定结构被破坏,使得颗粒间原有的空隙在外力作用下由于颗粒间的移动、旋转等方式被极大缩小,重新排列成较为致密的充填结构。这个阶段主要特征是以颗粒重排为主,粉体表观密度随压力增加迅速增加。
第二阶段,被压缩粉体密度随压力增加变化显著减缓。这一过程粉体颗粒间接触面积进一步增大,此时会给压缩过程带来一定阻力,如颗粒间的摩擦力、由于颗粒啮合造成的机械结构所导致的机械阻力等。
第三阶段,当负载到达一定程度并且颗粒间接触面积足够大时,粉体颗粒间的空隙已经很难再被压缩。此时继续增大负载,会在颗粒内部引起颗粒的弹性变形和塑性变形。当压力卸载后,能够恢复的变形部分即为弹性变形,不能恢复的变形部分为塑性变形。如果继续增大负载,此时颗粒会因为外力过大而发生破碎,分裂成更多更小的粉体颗粒。较小的破碎颗粒会进入大颗粒的空隙内。这一过程伴随着颗粒间的变形与颗粒破碎,将导致粉体密度随着压力变化继续上升。
总体来说,可将粉体压缩过程总结为:第一阶段粉体的压缩以颗粒间的位移为主;第二阶段主要发生颗粒的加工硬化;第三阶段以颗粒受压发生形变为主。
粉体压缩经典方程
由于粉体在压缩过程中所发生的机械啮合、弹性形变、塑性形变、颗粒破碎等过程,很难用单一的数学方程进行解释。因此研究者们尝试使用压缩过程中涉及的压力与粉体床层固结状态的性质如孔隙率,体积或密度,来描述粉体压缩过程,由此提出了多种用于描述粉体床层高度或体积变化与所施压力之间函数关系的经验公式。
1923年,Walker在研究金属粉末压缩过程中,提出了用于描述粉体体积变化与压力之间关系的Walker方程:
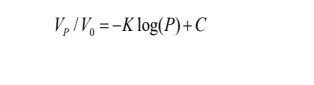
式中,VP,V0分别为压缩后粉体体积与空隙率为零时体积,P为轴向压力,K,C为常数,与粉体种类有关。Walker方程主要应用于金属粉体的相关研究中,适用于高压条件下粉体压缩行为的有关研究。
1961年,Heckel基于一级化学反应动力方程的假说将浓度和时间替换为孔隙率和压力,提出了可应用于描述金属及非金属粉体孔隙率与压力之间关系的Heckel方程:
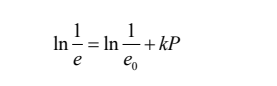
式中,e0,e分别为粉体自然状态下的空隙率与压力为P时的空隙率,k为常数,可以用来衡量粉体的可压缩性。Heckel方程是药物粉体压缩领域中常用的经验公式,用于描述粉体的相对密度与施加压力的变化关系。但有关文献指出,在较低压力和较高压力下,该方程存在一定误差,只有在中间压力阶段呈线性关系。
1971年,川北公夫根据陶瓷粉体的压缩规律,推导出粉体的相对体积与压力之间的Kawakita方程:
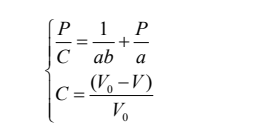
其中a和b均为常数,a是在压强P下粉体体积减小量,用于描述粉体的压缩性质。V0是粉体自然堆积状态下体积,V是在压强P下粉体压缩后的体积,C为粉体压缩前后体积变化率。Kawakita方程是在药物粉体压制成型中最常见的经验方程,并且川北方程还可以适用于粉体等静压成形、冲击成形等不同方式的压缩过程中,其适用于柔软松散即低压条件和高孔隙率的粉体压缩研究。
1980年,黄培云结合粉体压缩过程中会出现加工硬化的现象,并引入了时间因素对粉末压缩的影响,提出了双对数压制方程:
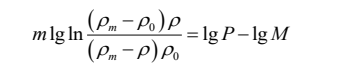
式中,ρ为压缩后粉体密度;ρ0为粉体松装密度;ρm为材料的理论密度;P为所用压强;M为压制模量;m为加工硬化指数,用来表征粉体压缩的难易程度。该方程在金属粉末冶金领域中得到了广泛应用,适用于硬质金属粉体的成型研究。
参考来源:
霍枫.粉体离心压缩过程仿真与动力学分析
(中国粉体网编辑整理/青黎)
注:图片非商业用途,存在侵权告知删除

2025-01-21
2025-01-17
2025-01-10
2025-01-08
2025-01-06
2024-12-30
2024-12-26
2024-12-25